Ex 2.59

Taking the union of two sets isn’t too difficult. We simply pick one set, and add every member of the other set to it. As long as we use adjoin-set to add the elements of the other set, we won’t need to worry about duplicate items.

Ex 2.60

Allowing for duplicate elements lets us simplify adjoin-set. It’s as simple as just using cons to add the item to the list. Similarly, union-set can be simplified to just an append operation. The other operators can remain unchanged. Also of note is that our test function sets-equal? does not change either, per our definition of set equality.

The non-duplicate set is strictly superior in terms of space. This also probably leads to better performance in time when using element-of-set?. The speed of the search depends on the size of the list used to store the set. This means that for situations when compact, easy-to-search sets are required, the first will be better.

The main advantage the duplicate-allowed version has is that adjoin is a much faster function. In a situation where elements are frequently added (and the speed of this operation is important) but infrequently accessed, the second version would likely be better. It might also be preferable when duplicates are in fact very rare. Then the time spent avoiding duplicates using the first method is effectively wasted, and the gain in search speed is minimal.

Ex 2.61

The way to save steps with ordered sets is to make comparisons and stop when we’ve gone far enough into the set. The ordered version of adjoin-set will add the new element as soon as it determines that the rest of the elements in the set are larger than it. Otherwise, it keeps searching. When the elements match, the element is not added and the set is returned unchanged. In contrast, the unordered version must search the entire set (by using element-of-set?) to determine if there is a duplicate.

Sometimes this means that the ordered version will only search a few elements, and sometimes it searches for more. If the elements are evenly distributed, then this will average out to searching through half the set. In the worst case, it will need to search the whole set, which is no worse than the unordered case.

Ex 2.62

In order to achieve Θ(n) in steps, we must examine each element of the sets only once. This process is analogous with the given implementation of intersection-set. In fact, it can be nearly identical; the only real difference is that when one of the sets is null, the other is returned.

Ex 2.63

The first procedure recursively moves down the left branch (without adding entries) until it reaches a leaf. As it backs out it will add first the root of the branch, and then move down the right branch until another left branch is found. By appending the center and right branch to the left branch’s entries, entries are added in the order left-branch, center, right-branch.

The second procedure moves through the list in sort-of the opposite direction, but constructs its results differently too. First the right branch is traversed until the right-most leaf is found. At this point the right leaf is added to the result-list. As it backs up the tree, each root entry is added to the head of the result-list, which gets passed to the left branch. Once the left-most branch is found, it will ‘jump’ up to the root of that branch. In the end, the entries actually end up in the same order as with the first method – left branches at the head, then the root (center) entry, then the right branches.

As for the time taken to convert a balanced tree, the second is faster, but not by a huge margin. The first procedure must make an append operation at each node. In a balanced tree, each node has 2 nodes below it, and will append half the tree below it at each depth. Let’s consider append as taking an O(n) number of steps. Then there will be on the order of n * log(n) total steps due to append since the tree depth is log n. There will be n steps for the cons operation, as each entry is added once. That makes the whole procedure O( n * (1 + log(n))). The second procedure simply moves through the tree and operates on each node only once, using cons. That makes the conversion O(n).

Ex 2.64

Skipping past the case when n is 0, the tree is formed by building the branches in steps. First, the number of required elements (less one) is divided in half, ignoring the remainder. This is used to create the left branch, by a recursive call to partial-tree that will build it from the first part of the list. Then the root and right branch are created. The size of the right branch is determined by subtracting the size of the left branch, and one for the root, from the required number n. That gives us a tree with the right number of elements, divided as evenly in half as possible. At each stage, the list of unprocessed elements is retained, and returned as part of the result. This is done so that the higher level does not need to worry whether the tree below has an exactly balanced number of elements, and this will cover cases where only a leaf is generated as well as those where a three-part tree is built.

Something to observe about this conversion is that in order for the tree to be structured with the expected order used by algorithms such as element-of-set?, the list itself must start out sorted. Elements are simply added to the tree without any checking. Creating a balanced tree from an unsorted list would require extra work, and for these exercises it’s easier to use a built-in list sort to ensure the expected result.

To show the resulting diagram and examine the procedure in more detail, let’s step through the process:

(list->tree '(1 3 5 7 9 11))

(partial-tree '(1 3 5 7 9 11) 6 )  ; The list is 6 elements long

; building the left tree at depth 0
	(partial-tree '(1 3 5 7 9 11) 2)  ; (6-1)/2 = 2
	
; building the left tree at depth 1
    	(partial-tree '(1 3 5 7 9 11) 0)  ; (2-1)/2 = 0
	
; This leads to an empty left tree.
; The center value is 1 (the first of the remaining elements)
; The right tree will be of size n - (left tree size + 1)  = 2 - (0 + 1) = 1
		(partial-tree '(3 5 7 9 11) 1)
; This call leads to an empty left tree  [size (1-1)/2], and an empty right tree [size 1 - (0 + 1)]
; This time the center entry is 3.

That gives us a left tree of size 2.

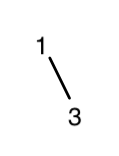
The center entry taken next is 5, and we will build a right tree of size (6 – (2+1)) = 3 from the remaining elements, (7 9 11).

This time we’ll have one element in the left-tree (7), one in the center (9), and then one in the right-tree (11).

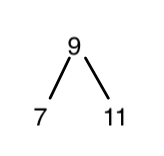
The final diagram, with 5 in the center, looks like this:

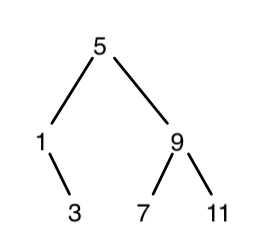
As for the order of growth of this operation, there are two main processes that must be considered. The first is the call to make-tree, which occurs once for each recursion on partial-tree. Since around half the list is processed with each recursive call, the number of these calls is O(log n). The other part is the processing of the list elements. It should be apparent that each element of the list is used in tree construction only once, as the car is taken and the cdr preserved at each step. This means the input list is processed once for each element, which is O(n). Since n grows much faster than log n, we can ignore the first part, and consider the whole procedure as O(n) in the number of steps required.

Ex 2.65

The indication to use the results of the previous two exercises should be a hint as to what to do here. Rather than write a whole new routine to process the trees, we can just convert them to [ordered] lists, and use the set operation procedures that are already written for sets, converting back to trees when the process is finished.

At first glance this seems like we’re only doing this to save having to write extra code. In fact this can be a relatively efficient process. We already know the ordered set operators are O(n) in time, and the conversion process is O(n) in both directions. Since the whole procedure just follows a set number of steps that are all O(n), the result of the whole process is O(n) in time. Generating a fast tree-based version that also produces balanced trees would require a fair deal of effort. Having the conversion option lets us re-use code and optimize for efficiency where it is needed.

Ex 2.66

The tree-based version can be patterned on element-of-set? as previously defined for trees. About the only other thing to mention is that I added a slight change in recovering the record: while the unordered list version just takes the car of the record, replacing it with an accessor value gives more options in how records are stored and retrieved. Refer to the solutions file for more details.

Supplemental: Timed Tests

Most of the analysis of orders of growth is best kept in the realm of analysis rather than experimentation, at least in an academic setting. However, it may still be worth examining a few practical results, both to ensure that our theories are correct, and to discover other factors affecting performance. For this reason, there’s an extra file (named “2_3_3_extra.rkt” and linked below) that runs comparison speed tests on a few different implementations. They all rely on a solutions file for this section, so either download mine or use your own. As the name suggests, the timing tests only work using Racket/Pretty Big.

In order to get a more ‘fair’ result, the tests are run in an alternating random order. The reason for this is that the time taken by the Racket interpreter can be affected by whatever was executing just before a test. This is primarily due to garbage collection, and while it isn’t entirely proper to exclude garbage collection time, the random test order can balance most other factors as well, so it is still worth doing.

While the interpretation of the timed results should be taken with a grain of salt, we do indeed see some correlation between our theoretical expectation and the actual results.

• The two tree-list conversion routines perform as expected. The first takes longer, and the growth correlates with log n .
• I made an attempt to show off the advantage of the ‘conversion’ approach to union and intersection for tree-based sets. If the operations attempt to operate directly on the trees, they can take considerably longer.
• Comparing the unordered vs. ordered versions with adjoin-set shows that the unordered version can actually be faster. Does this mean we failed in that exercise? Not exactly — recall that the exercise was looking for a reduction in the number of steps, not in time taken. As we’ve seen before, we can’t always be certain of the fact that any particular operation (or step) will be slower or faster. In this case, it’s likely the recursive process that preserves the first part of the set is taking more time than even searching the entire set.
• We do see a clear savings in steps resulting in a time savings in element-of-set? searches for the ordered vs. unordered versions, however.
• All that said, the savings of the tree version, with its log n growth, easily blows both of them away.

Solutions 2.3.3

Extra Timed Tests 2.3.3