SICP
SICP 2.5.3 (Extended) Solutions
September 16, 2016 11:13
Ex. 2.93
The main part of the exercise is simply changing all operations within the rational package to use the generic procedures instead of built-in Scheme procedures. Each + gets replaced with add, * with mul, etc. This change only needs to take place in the internal procedures like add-rat, demonstrating the usefulness of that abstraction. The constructors and the actual installed procedures don’t have to be rewritten.
The one place where the generic operations cannot be used is in the conversion to other types. We aren’t required to support generic operations in the integers and reals, but preserving the ability to raise or drop to those values is critical. The changes to rational must not disrupt how it used to work (with the exception of reducing to lowest terms, which is explicitly removed). We need to be able to actually convert the values, but only if it’s possible to do so.
To accomplish this, I re-used the method that helped solve a similar problem with complex numbers. The to-scheme-number procedure will get the value wrapped up in the package type’s ‘number’ so that it can be used by Scheme’s routines and passed to a constructor. By defining it for integers and reals, we can then project and drop the rational numbers. Here’s the code for project:
(put 'project 'rational ; to integer
; This can only be done with values that can be coerced,
; as quotient only works on Scheme numbers.
(lambda (x) (let ((num-n (to-scheme-number (numer x)))
(den-n (to-scheme-number (denom x)))
)
(if (and num-n den-n)
(make-integer (quotient num-n den-n))
false
)
)
)
)One change made was to have to-scheme-number return false when the value cannot be converted. This new version of project will check if the numerator and denominator were successfully converted before doing the Scheme operation of quotient on them. Polynomials cannot, in general, be converted, Constant-term-only polynomials could be handled so rationals that include them are excluded from raising and dropping.
With these routines in place, polynomials (or any other value) can be used as the components of rationals, and all previous operations on rationals will still work, aside from reduction to lowest terms. However, it does mean that not all rational numbers can be used with each other, since we could be mixing polynomial rationals with other numbers. I’ll have more to say on this at the end of this section.
Ex. 2.94
This exercise doesn’t require any difficult operations; it’s a matter of connecting up and calling the procedures correctly. Since there is already an internal procedure remainder, all remainder-terms needs to do is use it on the result from div-terms. The higher level gcd-poly is almost identical to the arithmetic operations: it verifies that the two polynomials are in the same variable, and then calls a term-list operation on them (gcd-terms here). Finally, the system operation greatest-common-denominator is just another instance of using apply-generic. Non-polynomial values can just rely on Scheme’s gcd procedure.
What’s notable is that in order to add these simple routines to the polynomials, a lot of ‘internal’ procedures need to exist in the package. It turns out that div-terms depends on both mul-terms and add-terms, and those in turn depend on low-level accessor routines like order and coeff. Even though none of these change, they need to be copied into the package, since they are not stored anywhere in between package updates. This is not a particular weakness of the design in itself — what would normally happen outside of this context would be that the install package would be kept in a single location or file, and updated for each new change without having to be copied.
I also took the time to redo subtraction at this point. Previously I had no term-list subtraction procedure, and it was handled only on the polynomial level using addition and negation. Since gcd-terms repeatedly calls div-terms, which will then require subtraction, I added the sub-terms procedure. It does the same process of addition and negation, but on a term-list level. This avoids the unnecessary step of creating intermediate polynomials to subtract term lists.
Ex. 2.95
When we do this operation, we get the following result:
(polynomial
sparse
x
(2 (rational (integer . 18954) integer . 2197))
(1 (rational (integer . -37908) integer . 2197))
(0 (rational (integer . 1458) integer . 169)))In a more conventional format, that is:
| 18954 | x 2 - | 37908 | x + | 1458 |
| 2197 | 2197 | 169 |
At first glance, that looks to be a jumble of almost random numbers. However, recall that we eliminated the reduction of rational values to simplest terms. If we reduce those fractions, we get something a little better:
| 1458 | x 2 - | 2916 | x + | 1458 |
| 169 | 169 | 169 |
The denominators all match, and if we compare 1458 and 2916, we find the second is twice the first. Considering the expected answer, we can restate the result as:
| 1458 | ( x 2 – 2 x + 1 ) |
| 169 |
It’s almost the answer we expected to see. It’s just scaled by the curious fraction 1458/169. So how did that get into the result? The answer is in the polynomial division algorithm. If we work out another example by hand, we notice something that occurs from the very first step.
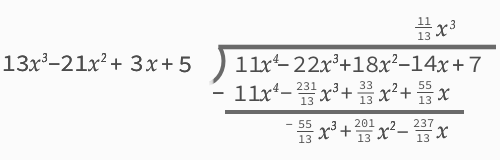
The algorithm will divide the coefficients by each other, and when they don’t divide evenly, the result will be a rational number. When multiplied by the remaining terms and added, the denominator will be present in all of them. As the division proceeds, the leading coefficient of the divisor will be multiplied every time. Even if we were reducing fractions, that factor will be introduced at each step, and will not be reducible unless it somehow divides every term of the dividend.
For polynomial division, the goal is not to produce integer results, but merely to eliminate the leading term by subtraction. It’s interesting to note that while this algorithm resembles the traditional long division algorithm, it works subtly differently, since we are not always able — or even trying — to select values that give us integers in the quotient. We can only eliminate the leading term of the dividend using the leading term of the divisor, and we do so using the reciprocal of their coefficients.
By way of comparison, we could apply the same method of ‘eliminating the leading term’ to division of a decimal value. Look at the difference in results if we worked in this fashion (effectively as a polynomial with x = 10), on a division problem that should have no remainder:
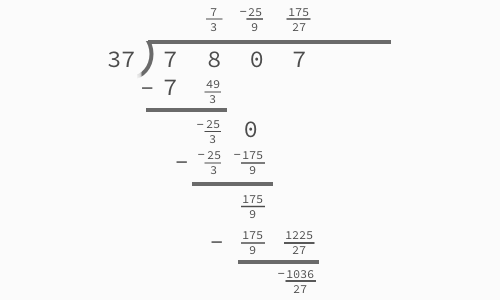
The result is a string of strange fractions. It looks to be just as much a mess as the GCD result, as it has the same sort of built-up fraction. But it does in fact sum to the proper quotient of 211 (despite the ‘remainder’). Similarly, as long as our system can store fractions properly, the calculated GCD result from the arithmetic system would indeed divide the two polynomials. Nothing actually is wrong with the method of division of polynomials. The problem goes a bit deeper than that.
Consider for a moment — just what does the ‘Greatest’ part of ‘Greatest Common Divisor’ mean when applied to polynomials? There is actually no way to order all the polynomials generally, as many are continually varying in value relative to each other. We can’t simply select the ‘largest’ polynomial from the set of those that divide two others. Unlike with integers, two polynomials cannot be reliably compared in size. With no generic meaning for ‘greater than’, it’s difficult to determine a GCD. We require a proper definition of what GCD means for polynomials, and it can’t rely on comparisons of their ‘value’ as with integers. The text glosses this by stating “the notion” of the GCD makes sense for polynomials (which it does), but only somewhat circularly implies that the GCD might have been the result produced by Euclid’s algorithm.
A proper definition of the GCD for the polynomials This definition applies to a broader class uses two rules, along with a strict definition of what division means.
By saying ‘A divides B’ what we mean is that there exists Q such that B = A * Q.
D is a GCD of P1 and P2 if these two conditions hold:
1. D divides both P1 and P2.
2. If C divides P1 and P2, then C also divides D.
Therefore D will be ‘greatest’ only in the sense that it includes all factors that divide both P1 and P2. For polynomials, there will normally be more than one GCD. That would seem to frustrate our attempts to compute and compare the GCD, but as it turns out, all GCDs of a given polynomial only differ from each other by a constant. That this is true isn’t too hard to show, since all GCDs must divide each other (see here for a proof of this along with several other statements that apply to polynomial division). But the very fact that multiple GCDs exist is the reason why we didn’t get the answer we expected.
Euclid’s algorithm gives us a GCD, but only one of an infinite possible number of them. What we need to do, then, is to decide on a process that can find a GCD without the build-up of messy rational values, especially since at some point we might have trouble storing the fractions with the desired precision. The remainder of the exercises will find a way to do this, and give us a ‘sensible’ GCD.
Ex. 2.96
This one is split into two sequential and distinct parts, so I’ll treat them in order.
2.96-a
This procedure is essentially the same as remainder-terms, but we need to compute the integerizing factor first. The only difficulty it presents is that we have to raise the first coefficient to the power determined by the order of the two polynomials. Since polynomial coefficients are in-system arithmetic values, we have two choices: Either implement exponentiation as a generic operation, or convert the coefficients and operate on them using Scheme procedures. While the first is arguably better as the operation could be useful in the system, I’ve gone the second route here, using to-scheme-number to force it into a value that will work with expt. That is a built-in math procedure that raises its first argument to the power of the second argument.
(define (pseudoremainder-terms a b)
(let ((intc (expt (to-scheme-number (coeff (first-term b)))
(- (+ 1
(order (first-term a))
)
(order (first-term b))
)
)
)
)
(remainder (div-terms (mul-term-by-all-terms (make-term 0 intc) a)
b
)
)
)
)Note that getting the exponent is easy, as we can use order on the terms. (The order procedure returns a Scheme integer, so no conversion is needed for it). The constructed integerizing factor is then put into a temporary constant term, which can be multiplied by the dividend term list using mul-term-by-all-terms, and that’s it for calculating the pseudoremainder.
That cleans up the rational values, but testing confirms that we still don’t get the GCD we want.
2.96-b
The integerizing factor is calculated by finding the GCD of the coefficients in a term list:
(define (gcd-coeffs tl)
(cond
((empty-termlist? tl) 1)
((< 2 (length tl)) (coeff (first-term tl)))
(else (greatest-common-divisor (coeff (first-term tl))
(gcd-coeffs (rest-terms tl))
)
)
)
)We have to use the generic greatest-common-divisor operation on the term list, since the coefficients are in-system values. It only allows two values at a time, so to figure it out from a list of more, I did it recursively. We takie the GCD of the rest of the list first, and then find the GCD of that and the first element. This is quite similar to most recursive procedures that use car and cdr on a list. One alternative might be to take elements of the list two at a time, and then repeat the process with a list that gets split in half each time.
I made a slight change to the exercise here, and didn’t even notice that I had done it until writing this up. Instead of modifying gcd-terms, I reduced the coefficients one step higher up, in gcd-poly. This is really a matter of style. To my mind, I don’t see the reduction step as a necessary element of computing gcd-terms, which is to say I’d rather keep it as it was and do the reduction outside of it. An argument could be made that all the GCD calculation should be performed at the lowest level, to keep the polynomial-level procedure simpler. It ultimately doesn’t appear to have an impact on performance of this procedure — modifying gcd-terms directly would mean changing the terminal branch from simply returning the value a to returning it with the GCD of the coefficients divided out.
Ex. 2.97
Once again, the steps here are a sequence of operations, so each is done in order.
2.97-a
I implemented the algorithm with a let at each major step. That allows for a sequence of calculations with each result being labeled. First, the GCD is computed. Next, the integerizing coefficient is calculated, using essentially the same method as in 2.96-a. This allows us to compute the (integerized) numerator and denominator with the GCD divided out. The coefficient GCD is then calculated, using gcd-coeffs from 2.96-b, and the generic GCD operation on the results from the two polynomials. This is finally converted to a constant term, and the returned result will have that constant divided out of both the numerator and denominator.
Incidentally, my earlier design decision (not changing gcd-terms to remove common factors) now turns out to have an effect on this procedure’s performance. I do compute the GCD of the terms, but also remove common factors from the fraction at the very end. That means that any earlier scaling down of the GCD coefficients would be to some extent ‘wasted’ effort. Since I don’t actually do it in gcd-terms, that is avoided in my solution. On the other hand, the ‘unreduced’ GCD may then produce a larger integerizing factor in the second step, which will lead to larger numbers in the multiplications. On balance, my approach is potentially a (minor) performance increase, since mathematical calculations are generally much quicker than running through the list an additional time.
The procedure reduce-poly is almost identical to div-poly, although I did not go so far as to create custom accessors analogous to quotient and remainder, and simply present the result as the list of the two reduced polynomials.
2.97-b
Adding a generic operation should come fairly easily now. The top-level procedure calls apply-generic with the operation. Each type that implements the operation needs to create an updated package. For the integers, there isn’t much else needed in the package. I did also create a reduce operation for complex, which is more of a ‘rationalization’ – it turns complex fractions into a single complex value with rational coefficients, by using the complex conjugate.
In calculating the reduced values, I also added in a reduced tag, which isn’t really necessary. It’s use was mostly for debugging, but there could be cases where knowing whether the value you have is reduced or not might help. To keep it from interfering with the existing generic operations, it’s defined to go away on any drop.
Here’s another observation that could extend this extension even further: We made a particular choice by forming only one GCD, as we know that multiple ones are possible. It’s sort-of implied in Exercise 2.95 that P1 could be anything, but consider for example if P1 was 2x2 – 6x – 4. If you run this through the same process as the exercise, you find that after the reduction step the result of the GCD procedure on Q1 and Q2 is not equal to P1 in this case. It will differ by a constant, since this P1 has a common factor in each term, and that gets removed when the GCD is computed. What, then, is the choice we made for the GCD? It’s the one with the smallest (in absolute value) integer coefficients. This has the advantage of ensuring that if we start with integer polynomials, they’ll stay that way, but other reasonable choices can be made about which GCD to produce (for instance, making a monic polynomial where the leading coefficient is always 1). The ‘correct answer’ here only matches because the first polynomial used for P1 met the same conditions as our choice for GCD. Whether we’d want to have a system that always satisfies the conditions of this exercise is certainly an open question.
With these new additions to the system, we’ve added to its complexity in a big way. Previously, we could use rational values in any operation. Now, however, we can’t really be certain whether a rational fraction is a numerical or a polynomial one (consider the headache of having a polynomial with a rational polynomial as a coefficient!). Allowing the mixing of types like this has the potential to really throw off everything done with them. In other words, we would have to continue to develop other features of the system in order to actually make this ‘generic’ system of rationals work consistently with all values it could produce. Of course, that’s well beyond the scope of this exercise set, but it’s worth keeping in mind that while the initial addition of functionality was relatively easy to implement thanks to our abstractions, there’s still quite a bit of complexity that would need to be explored to have a properly-implemented system.